[1일차] 기초 암호수학

[ 기초 정수론 ]

 

정수 (Integer)는 양의 정수, 음의 정수, 그리고 0을 포함하고 있는 집합을 의미한다.

 

정수론 (Number Theory)이란, 정수와 같은 수의 집합 상에서 덧셈(+)또는 곱셈(×)과 같은 연산을 정의하고

이 때의 특별한 성질에 대하여 연구하는 학문이다.

 

(예) 집합 {-1,0,1} ⊂ ℤ은 × 연산에 대하여 닫혀있다.

 

NOTE : 공개키암호시스템에서는 평문, 암호문, 키가 모두 하나의 정수이고 이들 간의 연산을 수행한다.

---

1. 나눗셈 정리

- 임의의 정수를 0이 아닌 정수로 나눈 몫과 나머지를 유일하게 정의할 수 있다는 정리

 

정수 a, b ∈ ℤ (b≠0) 에 대하여, a = qb + r (0≤r＜|b|) 를 만족하는 정수 q 와 r 이 유일하게 존재한다.

 

(예) a=7을 b=3으로 나눈 몫은 q=2, 나머지는 r=1이다. (7=3×2+1)

---

2. 최대공약수와 최소공배수

[ 약수 (factor) ]

두 정수 a, b에 대하여 b=ac를 만족하는 정수 c가 존재한다면, a를 b의 약수라고 하며, 이를 a | b와 같이 표기한다.

모든 정수는 1, -1을 약수로 가진다.

 

 

[ 배수 (multiple) ]

나눗셈 정리를 생각 했을 때, a = b×q+r 으로 표현할 수 있고 r=0이 된다.

b는 a의 약수이고, a는 b의 배수이다.

 

 

[ 최대공약수 (greatest common divisor) ]

두 정수 a,b에 대하여, d | a 이며 d | b를 만족하는 정수 d를 a와 b의 공약수(common divisor)라고 한다.

그리고 a, b ∈ ℤ에 대하여 다음 세 조건을 만족시키는 정수 d를 a와 b의 최대공약수라고 하고

기호로는 gcd(a, b)로 나타낸다.

(1) d > 0

(2) d는 a와 b의 공약수이다. 즉, d | a 이며 d | b 이다.

(3) 만약 c | a와 c | b이면, c ≤ d 이다.

 

 

[ 최소공배수 (least common multiple) ]

두 정수 a,b에 대하여, a | c 이며 b | c 를 만족하는 정수 c를 a와 b의 공배수 (common multiple)이라고 한다.

그리고 a, b ∈ ℤ에 대하여 다음 세 조건을 만족하는 정수 l 를 a와 b의 최소공배수라고 하고

기호로는 lcm(a, b)로 나타낸다.

(1) l > 0

(2) l은 a와 b의 공배수이다. 즉 a | l 이며 b | l 이다.

(3) 만약 a|c와 b|c 이면, l≤c이다.

 

 

[ 일차결합 ]

선형 결합 (Linear Combination) 이라고도 하며 벡터들을 스칼라베와 벡터 덧셈을 통해 조합하여

새로운 벡터를 얻는 연산을 말한다.

 

a ≠ 0 또는 b ≠0 일 때, d = gcd(a,b) 이면, 적당한 정수 x, y ∈ ℤ가 존재하여 d = ax+by가 된다.

즉, a, b의 최대공약수는 a와 b의 일차결합으로 표현된다.

 

(예) 정수 2와 3에 대하여 최대공약수는 gcd(2, 3) = 1이다.

그리고 1 = 2×2+(-1)×3으로 표현할 수 있다.

 

 

[ 유클리디안 알고리즘 (Euclidean algorithm) ]

유클리디안 호제법이라고도 불리는 유클리드 알고리즘은 두 정수가 주어졌을 때,

두 정수의 최대공약수를 두 정수의 일차결합으로 표현하는 방법을 찾을 수 있다.

따라서, 유클리디안 알고리즘을 이용하면 두 정수의 최대공약수 및 일차결합의 표현식을 손쉽게 찾아낼 수 있다.

 

a, b ∈ ℤ이고, a를 b로 나눈 나머지가 r이라고 하자. (여기서 a≥b이고, r은 0 ≤ r < b인 정수)

a와 b의 최대공약수를 (a, b)라고 하면, 다음이 성립한다.(a, b) = (b, r).

 

(예) 78696과 19332의 최대공약수를 구하면 다음과 같다.

 

 

 

[ 확장 유클리디안 알고리즘 (Extended Euclidean algorithm) ]

유클리디안 알고리즘의 과정을 반대로 이용하면 gcd(a, b) = ax + by 를 만족하는 정수 x와 y를 구할 수 있다.

 

배주 항등식 (Bezout's Identity)는 gcd(a, b) = d라고 할 때,

(1) ax + by = d를 만족하는 정수 x, y가 존재한다.

(2) d는 정수 x, y에 대하여 ax+by로 표현할 수 있는 가장 작은 정수이다.

(3) ax + by 로 표현될 수 있는 모든 정수는 d의 배수이다.

---

3. 소수와 소인수분해

양의 정수 p > 1 의 약수가 ±1 과 ±p 뿐일 때, p를 소수(prime number)라 한다.

또한 소수가 아닌 정수 a > 1 를 우리는 합성수 (composite number)라 한다.

 

(1) 소수 (prime) 중에 짝수는 2가 유일하다.

(2) 마지막 자리수가 5인 소수는 5가 유일하다.

(3) 1보다 큰 정수는 어떤 소수에 의해 나누어진다.

(4) 1보다 큰 정수는 소수의 곱으로 나타낼 수 있다.

 

소수는 무한히 많다.

 

[ 소인수 분해 ]

양의 정수 n이 소수이거나 또는 유한개의 소수들의 곱으로 나타내어지는 합성수 일 때, n은 소인수분해 된다고 말한다.

서로 다른 소수 pi만을 이용하여 표현하면

 

 

 

임의의 정수 n > 1은 소인수 분해된다. 만일

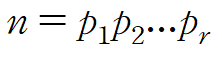
와

를 n의 소인수 분해라고 하면, r=s이고

두 소인수 분해는 인수의 순서만 다르다.

 

NOTE : 소인수 분해 정리를 때로는 계산의 기본정리 (The fundamental theorem in arithmetic)이라고 불릴 만큼,

정수의 성질에서 가장 기본이 되는 것 중에 하나이다.

 

[ 서로소 (Relative Prime) ]

서로소는 두 개 이상의 정수와의 관계를 의미한다. 다시 말해, 두 개 이상의 정수가 주어졌을 때 이 두 개의 정수가

서로소인지 아닌지를 따질 수 있다. 서로소는 주어진 정수들끼리 최대공약수 (gcd)가 1인 관계를 의미한다.

서로소에 대한 정확한 정의는 다음과 같다.

 

정수

가 주어졌을 때,

을 만족시키면, 이들이 서로소라고 한다.

특히, 두 정수 m, n의 최대공약수가 1이라면 이 두 정수가 서로소라고 한다.

 

---

4. 합동식, 중국인의 나머지 정리, 이차잉여

[ 모듈러 연산 (Modular arithmetic) ]

모듈러 연산(Modular arithmetic)은 법 연산이라 불리기도 한다.

정수 a에 대하여 양의 정수 m이 있다고 하면, a에 대한 모듈러 m에 대한 연산 결과는 a를 m으로 나누었을 때

나머지 값을 의미하며, 나머지가 n이라고 한다면 아래와 같은 수식으로 표현할 수 있다.

 

[ 합동식 ]

정수 a, b, m에 대하여 m|(a-b) 일 때, a는 모듈러 m에 대하여 b와 합동 (Congruence)이라고 한다.

이 때, 기호로는 다음과 같이 표현한다.

 

[ 완전 잉여계 ]

또한, 완전 잉여계의 각각에서 n과 서로소인 정수들로 이루어진 집합을 모듈러 n에 관한 기약 잉여계라고 한다.

 

(예) 모듈러 8에 대하여,

완전 잉여계 : 0, 1, 2, 3, 4, 5, 6, 7

기약 잉여계 : 1, 3, 5, 7

 

[ 오일러 phi ]

1부터 n까지의 정수 중에서 n과 서로소인 원소들의 ℤ*n라고 할 때, ℤ*n에 속한 원소들의 개수를 Φ(n)으로 표시하고

오일러 phi라고 부른다.

 

만약 소수 p에 대하여 오일러 함수 Φ를 계산하면,

 

 

[ 합동 방정식 ]

방정식 (equation)은 미지수가 포함된 식에서, 그 미지수에 특정한 값을 주었을 때만 성립하는 등식이다.

이 때, 방정식을 참이 되게 하는 또는 성립하게 하는 특정 값을 해 또는 근이라 한다.

따라서, 방정식이 주어졌을 때 방정식이 참이 되게 하는 근을 찾는 행위를 방정식을 푼다고 이야기 한다.

 

합동 방정식은 방정식이 등식으로 성립하는 관계의 해를 찾는 것이 아니라, 합동이 성립하는 경우의 해를 찾는 것이다.

x에 관한 일차합동방정식은 다음과 같다.

 

 

[ 항등원 ]

임의의 수 a에 대하여 어떤 수를 연산 *를 수행 하였을 때 처음의 수 a가 되도록 만들어 주는 수를 말하며,

항등원 e로 표현한다.

- 완전 잉여계 ℤn과 모듈러 n에 대한 + 연산에 대한 항등원은 0이다.

- 기약 잉여계  ℤ*n과 모듈러 n에 대한 × 연산에 대한 항등원은 1이다.

 

[ 역원 ]

두 원소를 연산한 결과가 항등원일 때, 한 원소에 대하여 다른 원소의 역원이 된다.

- 완전 잉여계 ℤn과 덧셈 + 연산에 대하여, 원소a의 항등원은 0 이되고 역원 -a 이다.

 

 

[ 중국인의 나머지 정리 ]

연립 선형 합동식의 공통 해를 찾는 문제를 우리는 중국인의 나머지 정리를 이용하여 해결할 수 있다.

이와 같은 조건을 만족하는 x를 찾기 이전에 존재 유무부터 확인을 해야 한다.

또한, 해가 존재한다고 하더라도 다수의 해가 존재하지 않는지 확인할 필요가 있다.

 

 

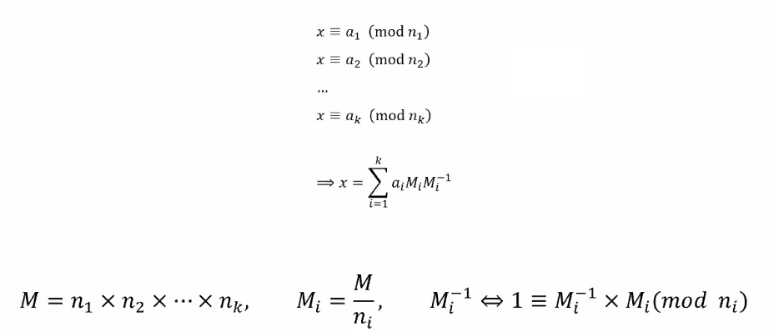
[ 이차잉여 ]

연립 일차 합동 방정식에 이어서, 이차 합동 방정식에 대하여 알아보자.

다음과 같은 형태를 갖는 방정식을 이차 합동 방정식 또는 이차 합동식이라 부르며, 이 때 방정식의 해 x는

존재하지 않거나 존재한다면 반드시 서로 합동이 아닌 두 개의 해를 가진다.

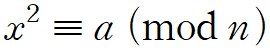
이차 합동 방정식이 주어졌을 때, 이 방정식이 해를 갖는다면 a를 이차잉여 (Quadratic Residue)라고 하며,

해를 갖지 않는다면 이차 비잉여 (Quadratic Nonresidue)이라 한다.

또한, 원소의 개수가 p-1개인 기약 잉여계 ℤ*n에 대하여 이차 잉여와 이차 비잉여의 개수는 정확하게 (p-1)/2 개로 같다.

 

 

[ 오일러 판정법 ]

이차 합동식에 대하여 해가 존재하는 경우와 존재하지 않는 경우를 각각 이차 잉여류, 이차비잉여류라 하였다.

모듈러 n 상에서 곱셈연산으로 정의된 군에서는 이차방정식의 해가 존재하지 않을 수 있음을 이해하였다.

오일러 판정법을 이용하면 주어진 방정식에 대한 이차잉여류와 이차비잉여류 여부를 간단하게 확인할 수 있다.

---

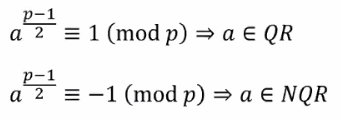
5. 위수, 원시근, 제곱-곱 연산 방법

[ 위수 (order) ]

gcd(a,n)=1을 만족하는 정수 a에 대하여,

이 되는 최소의 양의 정수 k를 모듈러 n에 대한 a의 위수 (order)라 부른다.

다시 말해, 모듈러 n에 대한 a의 위수를 |a| ≡ k (mod n) 으로 표기한다.

 

 

[ 원시근 (primitive root) ]

원시근에 대한 개념은 위수에 대한 이해가 필요하다. 오일러 정리에 따르면 n과 서로소인 a는 모듈러 n에 대하여

을 만족한다.

하지만 a의 거듭제곱을 Φ(n)보다 더 적은 횟수만을 수행하여 모듈러 n에 대하여 1을 만들 수 있음을 확인하였다.

 

모듈러 n에 대하여 a의 위수가 Φ(n)일 때, 즉 다음과 같을 때

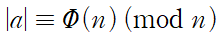
a는 모듈러 n의 원시근 (primitive root)라고 부른다.

 

 

[ 제곱-곱 연산 방법 ]

대부분의 공개키 암호 시스템에서는 모듈러 n에 대하여 a의 지수 연산을 수행한다.

위 식과 같이 지수 연산은 a를 거듭해서 곱해 나가면서 결과 값을 계산한다.

이는 상당히 큰 지수를 사용하는 공개키 암호 시스템에서 알고리즘의 수행속도를 좌우하는 핵심 부분이 된다.

따라서 공개키 알고리즘을 구현하는 대부분의 경우,

제곱-곱 연산방법을 적용하여 알고리즘의 수행시간을 줄여주고 있다.

이러한 제곱-곱 연산방법을 고속 지수 연산 (fast exponentiation)이라고도 한다.

 

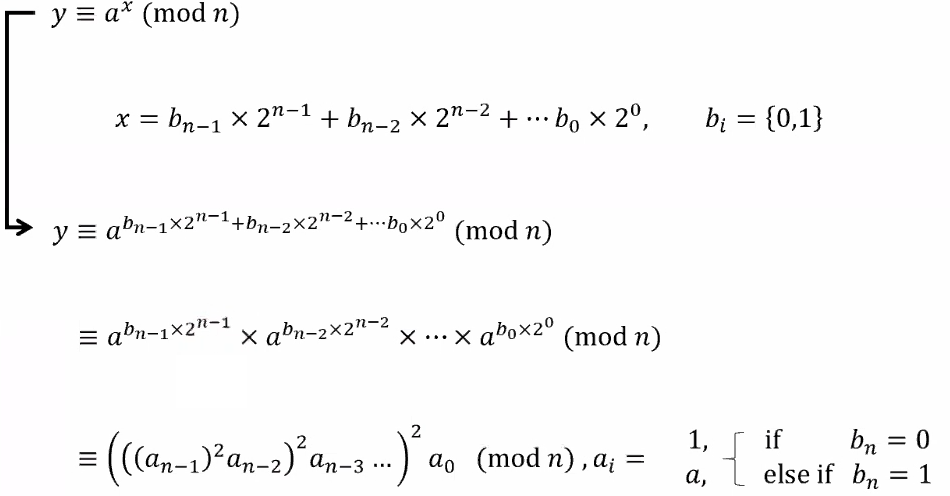
제곱-곱 연산 방법을 적용하는 경우 Hamming weight가 적은 지수를 사용하여야 곱셈 연산이 줄어드는 것을 알 수 있다.

즉, 지수의 수가 더 크다고 할지라도, Hamming weight가 적은 지수는 더 빠른 계산을 할 수 있다.

---

6. 소수판정법

소수 (prime number)는 양의 약수가 1과 자기 자신 뿐인 1보다 큰 자연수로 정의된다.

소수의 재미난 성질로 인하여, 수학에서 소수와 관련된 다양한 정리들이 나왔다.

또한 아직까지 해결되지 못한 채 수백 년 동안 가설로 남아있는 문제들이 많이 있다.

 

주어진 수가 소수인지 합성수인지를 판정하는 문제는 매우 간단해 보이지만, 정확한 정답을 제시하는 것은

어려운 문제로 알려져 있다. 소수 여부를 판단해주는 것이 어렵기 때문에, 숫자가 큰 소수를 찾는 것도 어렵고

합성수가 주어졌을 때 이를 소인수분해 하는 것도 모두 어려운 문제이다.

 

 

[ 에라토스테네스의 체 ]

특정 범위 n 안에 있는 소수들을 찾기 위한 가장 간단한 방법은 다음과 같은 에라토스테네스의 체가 있다.

(1) 1을 제외하고 찾고자 하는 범위의 자연수를 나열한다.

(2) 2의 배수를 지워나간다.

(3) 다음 수의 배수를 모두 지운다.

 

 

[ 페르마 소수 판정법 ]

현재 사용되는 소수 판정법들 중 대부분 17세기 페르마가 생각해낸 것과 유사한 개념에서 출발한다.

페르마의 소정리에 따르면 p가 2보다 큰 소수인 경우에 2^(p-1)-1은 p로 나누어 떨어진다.

그러므로 p의 소수 여부를 판정할 때, 2^(p)-2가 p로 나누어 떨어지지 않으면 p는 소수가 아님을 알 수 있다.

 

 

[ 의사소수 (psudoprime) 판정법 ]

페르마의 소정리의 역을 생각해보자.

 

" 어떤 정수 n과 서로소인 모든 a에 대해 a^(n-1)≡1 (mod n)이 성립하면 n은 소수이다. "

 

양의 정수 a에 대하여

을 만족하는 수 n을 밑수 a에 대한 의사소수 (psudoprime)라고 한다.

 

자연수 n에 대한 판정을 할 때 소수가 아니라는 판정을 하는 경우 100% 확률로 소수가 아니게 되고,

소수라고 판정하는 경우 k%의 실패 확률을 가지고 소수로 판정하는 방법이다.

 

 

[ 밀러-라빈 소수 판정법 ]

페르마 소수 판정법과 마찬가지로, 밀러-라빈 소수 판정법도 소수가 갖고 있는 특별한 성질을 이용한다.

p가 2보다 큰 소수인 경우 p-1은 짝수가 된다. 따라서 2^(s)d의 형태로 나타낼 수 있다.

이 때, s는 정수이고 d는 홀수이다.

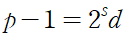
여기에 페르마의 소정리를 이용하면 p와 서로소인 a에 대하여 다음 2가지 식 중 한 가지가 성립하게 된다.

 

p와 서로소인 a에 대하여 다음 두 가지 식이 성립하면 a는 p가 합성수라는 것을 100% 확신할 수 있는 증거가 된다.

만약 두 식이 성립하지 않으면 p는 a에 대하여 의사소수가 된다.