SH1R0_HACKER
RSA Starter 1 본문
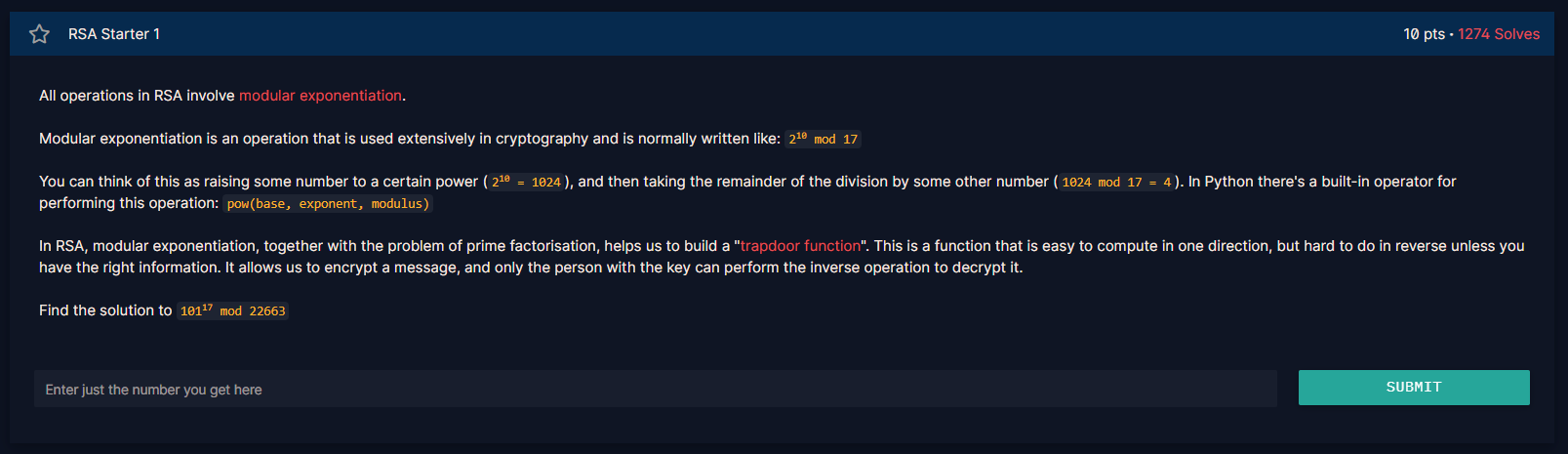
RSA의 모든 연산은 modular exponentiation을 포함합니다.
모듈러 제곱법은 암호학에서 광범위하게 사용되는 연산이며 일반적으로 2^(10) mod 17과 같이 쓰여집니다.
여러분은 숫자를 (2^(10) = 1024) 로 만든 다음에 (1024 mod 17 = 4)와 같이 나머지를 얻는다고 생각할 수 있습니다.
Python에서는 이러한 연산을 하기 위한 내장된 연산자가 있습니다. pow (밑, 지수, 모듈러스)
RSA에서 모듈러 제곱법은 prime factorisation 문제와 함께 "trapdoor function"을 만드는데 도움이 됩니다.
이것은 한 방향으로 계산하기 쉽지만 정확한 정보를 가지고 있지 않다면 역방향으로 계산하기엔 어렵다.
그것은 우리가 메세지를 암호화 할 수 있도록 해주고, 키를 가진 사람만이 그것을 해독하기 위해 역연산을 할 수 있다.
101^(17) mod 22663에 대한 답을 찾아라.
이 문제는 그냥 파이썬을 사용하면 쉽게 풀 수 있다.
그러나 우리는 모듈로 거듭제곱법에 대해 자세히 알아보자.
하지만 위의 문제와 같이 101^(17)을 22663으로 나눈 나머지를 알고싶다면 일반적인 방법으로는 무리가 있다.
이걸 빠른 모듈러 제곱법 (Fast Modular Exponentiation)을 이용하여 풀어보면 간단하게 풀린다.
참고 블로그 :
[정수론] 빠른 모듈로 거듭제곱법 - fast_mod_exponentiation/ python,c
빠른 모듈로 제곱법 - fast_mod_exponentiation 일반적으로 a^e의 mod n 을 계산하는 알고리즘을 떠올려봅시다. 만약 2^5 을 3으로 나눈 나머지를 알고 싶다면, 먼저 2를 5번 곱해서 32를 계산한뒤에 32를 3으�
man-25-1.tistory.com
'Crypto > Cryptohack : General' 카테고리의 다른 글
| XOR : XOR Properties (0) | 2020.10.24 |
|---|---|
| XOR : Favourite byte (0) | 2020.10.24 |
| RSA Starter 2 (0) | 2020.10.21 |
| MATHEMATICS : Extended GCD (0) | 2020.10.18 |
| MATHEMATICS : Greatest Common Divisor (0) | 2020.10.18 |
